벡터 in Java

얼마전에, 한 기업의 입사 코딩 테스트를 보았다. 결론부터 이야기하자면, 기하학적, 이차함수에 대해 학습을 소홀히 하였고, 덕분에 시원하게 말아먹었다. 문제내용은, 법적인 이슈로 공개할 순 없다. 다만 해당 문제를 풀기 위해선, 기하학적 지식, 그리고, 기하학에서 벡터의 개념과 활용, 그리고, 삼각함수에 대한 지식과 그걸 코드로 자유롭게 표시할 능력이 있어야 했다. 비록 시험은 아쉽게 되었지만, 기본기에 대해 구체적으로 부족한 부분을 깨닫고, 매너리즘에 빠질 무렵에 아주 제대로 동기부여를 한 것 같다. 이번 문서를 통해, 삼각함수와 벡터에 대한 개념을 짚어보고, 여러가지 간단한 상황을 제시하여, 코드로 풀어보는 시간을 가져보겠다.

용어

벡터 (vector)

위키피디아의 내용을 따르면, 분야에 따라 매우 다양하다. 생물학, 의학과 같이 현재 알고 싶어하는 분야와 관련없는 부분만 제외하면, 벡터는 다음과 같은 의미를 가진다.

• 물리학과 공학에서는 방향과 크기를 나타낸다.
• 선형대수학에서는 벡터 공간의 원소를 일컫는다.
• 컴퓨터에서는 화상의 표현 요소로서 방향을 지닌 선, 선 그림
• 동적 배열 자료구조

문제해결에 필요한 부분만 따로, 분류를 해보았는데, 지금 나의 상황에서 도움이 되는 부분은 크기와 방향, 선인듯 하다.

벡터의 내적(Dot Product)

벡터의 곱을 정의하는 개념 중 하나로, 또 다른 것으로, 외적이 있다. 그런데, 외적의 경우, 고등수학을 뛰어넘는다. 이 부분에 대해서 기억해둘 점은 다음과 같다.

• 내적은 한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다.

  • 

• 

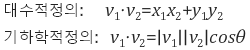
• 대수적정의와 기하학적정의를 통해 얻는 벡터의 내적의 값은 동일하므로, 이 두 가지의 수식을 활용하여, cos theta값을 구할 수 있고, 이걸 역 코사인화하여, theta값을 구할 수 있다.